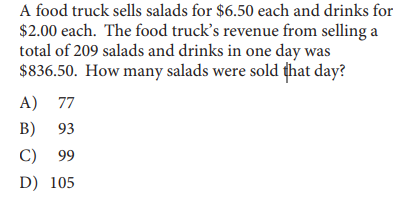A food truck sells salads for $6.50 each and drinks for
$2.00 each. The food truck’s revenue from selling a
total of 209 salads and drinks in one day was
$836.50. How many salads were sold that day?
A food truck sells salads for $6.50 each and drinks for $2.00 each. The food truck’s revenue from selling a total of 209 salads and drinks in one day was $836.50. How many salads were sold that day?
Answer:
To determine how many salads were sold, we need to set up a system of equations using the information provided:
- Equation for the number of items sold:
Let ( s ) be the number of salads sold and ( d ) be the number of drinks sold.
s + d = 209
- Equation for the total revenue:
The revenue from salads ($6.50 each) and drinks ($2.00 each) totals $836.50.
6.5s + 2d = 836.5
Now, we have the system of linear equations:
\begin{cases}
s + d = 209 \\
6.5s + 2d = 836.5
\end{cases}
To solve this system, we can use the substitution or elimination method. Here, we’ll use substitution:
- From the first equation, solve for ( d ) in terms of ( s ):
d = 209 - s
- Substitute ( d = 209 - s ) into the second equation:
6.5s + 2(209 - s) = 836.5
- Simplify and solve for ( s ):
6.5s + 418 - 2s = 836.5
4.5s + 418 = 836.5
4.5s = 836.5 - 418
4.5s = 418.5
s = \frac{418.5}{4.5}
s = 93
Therefore, the number of salads sold is ( \boxed{93} ).
To ensure correctness, let’s verify the solution:
- If ( s = 93 ), then ( d ) can be calculated as:
d = 209 - 93 = 116
- Check the total revenue:
6.5 \times 93 + 2 \times 116 = 604.5 + 232 = 836.5
Since both the number of items and the total revenue are correct, the solution ( \boxed{93} ) salads is accurate.
1 Like