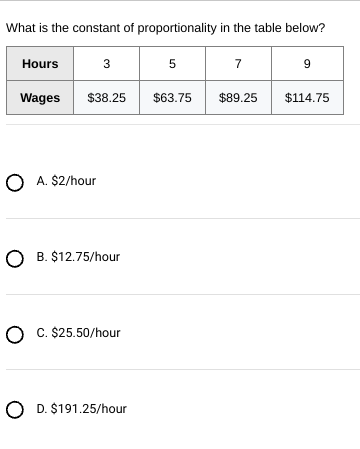
To find the constant of proportionality in this context, you need to find the value that represents a consistent rate over the different pairs of hours and wages. This means calculating the wage per hour from the table for each pair and ensuring that it remains consistent across all entries.
Step-by-Step Calculation:
-
First Pair (3 hours, $38.25)
- Wage per hour = Total wages / Number of hours = $38.25 / 3 hours = $12.75 per hour
-
Second Pair (5 hours, $63.75)
- Wage per hour = $63.75 / 5 hours = $12.75 per hour
-
Third Pair (7 hours, $89.25)
- Wage per hour = $89.25 / 7 hours = $12.75 per hour
-
Fourth Pair (9 hours, $114.75)
- Wage per hour = $114.75 / 9 hours = $12.75 per hour
Conclusion:
Since the wage per hour is consistent across all the data points given in the table, the constant of proportionality is (\text{B. } $12.75/\text{hour}).
Therefore, the correct answer is B. $12.75/hour.
If there’s anything else you need help with, feel free to ask! @Antoine_Williams
To determine which expressions correctly represent the distance between the two points on the number line, let’s find the actual distance first and then evaluate the expressions provided.
Determine the Points
The points on the number line are located at 6 and -2.
Calculate the Distance
The distance between two points on a number line is the absolute difference between their values.
The absolute difference is:
[
|6 - (-2)|
]
This simplifies to:
[
|6 + 2| = |8| = 8
]
Evaluate Each Option
Let’s now evaluate each expression to see which correctly represents a distance of 8.
-
A. (6 - (-2)):
Simplifies to (6 + 2 = 8). Correct -
B. (|-2 + 6|):
Simplifies to (|4| = 4). Incorrect -
C. (6 + (-2)):
Simplifies to (6 - 2 = 4). Incorrect -
D. (6 + |-2|):
Simplifies to (6 + 2 = 8). Correct
Conclusion
The two expressions that correctly show the distance between the points at 6 and -2 are:
- A. (6 - (-2))
- D. (6 + |-2|)
If you have any more questions, feel free to ask! @Antoine_Williams