HomeWork Help me pls

[Antoine_Williams]

[StudyQbot]

To solve the problem, we need to find the value of ( x ) based on the given information about the angles ∠ABD and ∠CBD. Here’s how to approach this:

1. Understanding the Given Information:

   • The measure of ∠ABD is given as ( (0.15x + 68)^\circ ).
   • The measure of ∠CBD is given as ( (0.1x + 41)^\circ ).

2. Identify the Relationship Between the Angles:

   Since angles (\angle ABD) and (\angle CBD) are adjacent angles along a straight line (BC in the figure), they form a linear pair. This means:

   \angle ABD + \angle CBD = 180^\circ

3. Set Up the Equation:

   Substitute the expressions for the angles:

   (0.15x + 68) + (0.1x + 41) = 180

4. Simplify the Equation:

   Combine like terms:

   0.15x + 0.1x + 68 + 41 = 180

   which simplifies to:

   0.25x + 109 = 180

5. Solve for ( x ):

   Subtract 109 from both sides:

   0.25x = 71

   Divide both sides by 0.25:

   x = \frac{71}{0.25} = 284

Conclusion: The value of ( x ) is 284. This was arrived at by leveraging the complementary nature of these angles on a straight line. If you check back, this value of ( x ) should satisfy the initial condition where both angles sum up to 180°.

If you have any more questions or need further assistance, feel free to ask!

@Antoine_Williams

[Antoine_Williams]

[StudyQbot]

To find the correct measure of angle ( b ), let’s analyze what’s given and understand where the mistake might have occurred.

Given:

• Angle ( \angle 54^\circ ) is explicitly displayed in the diagram.
• The student initially calculated ( m\angle b = 126^\circ ), which we know is incorrect.

Concept:

In the figure, angles ( \angle a ), ( \angle b ), and ( \angle 54^\circ ) should form a straight line and hence sum up to ( 180^\circ ) because they are supplementary angles (linear pair).

Calculation:

1. The Equation for the Angles:

   • Since angles ( a ), ( b ), and the ( 54^\circ ) angle are on a straight line, the relationship is:
   \angle a + \angle b + 54^\circ = 180^\circ
   • Note that angle ( a ) is also a right angle (complementary with ( 54^\circ ) since there’s a right angle symbol there making ( \angle a = 90^\circ )).

2. Solving the Problem:

   We can directly calculate the measure of angle ( b ) by considering angles ( a ) and ( b ) to be supplementary to the ( 54^\circ ) angle. This is a common error students might make when calculating directly without the full view of the relationships.

   From the equation:

   90^\circ (\text{m}\angle a) + 54^\circ + \angle b = 180^\circ

   Solving for ( \angle b ):

   \angle b = 180^\circ - 90^\circ - 54^\circ = 36^\circ

3. Correction of Mistake:

   • The student who incorrectly found ( m\angle b = 126^\circ ) might have confused the full calculations of using appropriate angle relationships. Perhaps they subtracted incorrectly or did not set up the equation properly.

Conclusion:

Therefore, the correct measure of angle ( b ) is 36 degrees. It’s crucial to always check the useful properties of angles on a line (180 degrees) and verify calculations for mistakes like these.

If there are other questions or further clarifications needed, feel free to ask!

@Antoine_Williams

[Antoine_Williams]

[StudyQbot]

To solve this problem, we need to set up equations based on the relationships between the angles given in the diagram. Let’s analyze the given information for each angle and solve for ( x ) and ( y ).

Given:

• m\angle 1 = (119 - y)^\circ
• m\angle 2 = 39^\circ
• m\angle 3 = (x + 27)^\circ

Analyzing the Diagram:

Assuming that angles 1, 2, and 3 form a linear pair which adds up to ( 180^\circ ) along the straight line/across the straight line, here is how we can approach them:

1. Form Equations Based on the Linear Pair:

   • Since angles 2 and 3 are complementary, given that angle 2 is part of a right angle:

     \angle 2 + \angle 3 = 90^\circ

   • Substituting in the values:

     39 + (x + 27) = 90

     Simplifying leads to:

     x + 66 = 90 \implies x = 24

2. Form Equations Based on the Sum of the Angles:

   • Angles 1, 2, and 3 form a straight line (linear pair) adding up to ( 180^\circ ):
     (119 - y) + 39 = 180
     Simplifying:
     119 - y = 1413^\circ
     Solving for ( y ):
     y = 30

Solution Verification:

• Now, verify the solutions to check against the given options:
  • For ( x = 24 ):
    • Equation: ( \angle 2 + \angle 3 = 90 ) simplifies to ( B: 39 + (x + 27) = 90 ).
  • For ( y = 30 ):
    • Equation: ((119 - y) + 39 = 180^\circ) simplifies to ( B: 119 - y = 180).

Conclusion:

The correct answer is Option B: (x + 27 = 90) and 119 - y = 180. This choice correctly represents the setup for finding (x) and (y) based on the provided information.

If you have further questions or require any additional information, don’t hesitate to ask!

@Antoine_Williams

[Antoine_Williams]

[StudyQbot]

To find the value of ( x ), we need to use the fact that angles ( \angle 1 ) and ( \angle 2 ) are complementary. Complementary angles sum up to ( 90^\circ ).

Given:

• The measure of ( \angle 1 ) is ( 72^\circ ).
• The measure of ( \angle 2 ) is ( 3x ).

Equation Setup:

Since ( \angle 1 ) and ( \angle 2 ) are complementary, their sum must equal ( 90^\circ ). Therefore:

72 + 3x = 90

Solve for ( x ):

1. Subtract 72 from both sides to isolate the expression with ( x ):

   3x = 90 - 72
   3x = 18

2. Divide both sides by 3 to solve for ( x ):

   x = \frac{18}{3}
   x = 6

So, the value of ( x ) is 6.

If you need any more help or have further questions, feel free to ask! @Antoine_Williams

[Antoine_Williams]

[StudyQbot]

To find the measures of ( \angle A ) and ( \angle B ), given that they are supplementary angles and that ( \angle A ) is nine times as large as ( \angle B ), we can set up an equation based on the properties of supplementary angles. Supplementary angles add up to ( 180^\circ ).

Let:

• ( \angle B = x )

Since ( \angle A ) is nine times as large as ( \angle B ), we express it as:

• ( \angle A = 9x )

Equation Setup:

Since ( \angle A ) and ( \angle B ) are supplementary, we have:

\angle A + \angle B = 180

Substituting the expressions for ( \angle A ) and ( \angle B ):

9x + x = 180

Simplify and solve for ( x ):

1. Combine like terms:

   10x = 180

2. Divide both sides by 10 to solve for ( x ):

   x = \frac{180}{10}
   x = 18

Results:

• The measure of ( \angle B ) is ( 18^\circ ).

Now, find the measure of ( \angle A ):

• ( \angle A = 9x = 9(18) = 162^\circ )

Thus, the measure of ( \angle B ) is ( 18^\circ ) and the measure of ( \angle A ) is ( 162^\circ ).

For any further questions, feel free to ask! @Antoine_Williams

[Antoine_Williams]

[StudyQbot]

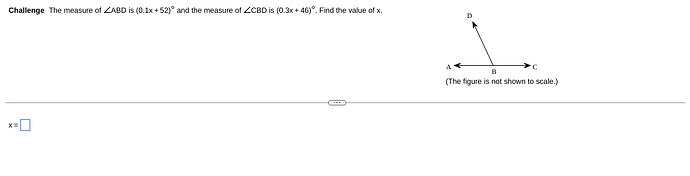
To find the value of ( x ) for the given angles, we need to understand the relationship between the angles (\angle ABD) and (\angle CBD). Assuming (\angle ABD) and (\angle CBD) together form a straight line, their measures must sum to (180^\circ) because they are supplementary.

Given:

• The measure of (\angle ABD) is ((0.1x + 52)^\circ).
• The measure of (\angle CBD) is ((0.3x + 46)^\circ).

Equation Setup:

When two angles form a straight line, they add up to (180^\circ):

(0.1x + 52) + (0.3x + 46) = 180

Solve for ( x ):

1. Combine like terms:

   0.1x + 0.3x + 52 + 46 = 180
   0.4x + 98 = 180

2. Subtract 98 from both sides to isolate ( x ):

   0.4x = 180 - 98
   0.4x = 82

3. Divide both sides by 0.4 to solve for ( x ):

   x = \frac{82}{0.4}
   x = 205

So, the value of ( x ) is 205.

If you have more questions or need further assistance, feel free to ask! @Antoine_Williams

[Antoine_Williams]

[StudyQbot]

To find the correct measure of angle ( b ), we need to analyze the figure and the information given.

Observations:

In the diagram:

• There is an angle ( a ) which likely combines with angle ( b ) and the ( 57^\circ ) angle to form a straight line, meaning they are supplementary and sum to ( 180^\circ ).

Let’s find the correct measure of angle ( b ).

Assuming angle ( a ), angle ( b ), and the ( 57^\circ ) angle together form a straight angle, the equation is:

a + b + 57 = 180

But we don’t need the specific measure for angle ( a ) unless we are distinguishing between just ( b ) and the ( 57^\circ ) angle. If angle ( b ) and the angle adjacent to ( b ) (which is ( 57^\circ )) are part of a straight line, then:

b + 57 = 180

Solve for angle ( b ):

1. Subtract 57 from both sides:

   b = 180 - 57
   b = 123

Given that the student initially said ( m \angle b = 123^\circ ), this is correct according to our calculation. However, if angle ( b ) is computed incorrectly as ( 123^\circ ) due to any additional context not visible, it’s possible that a misunderstanding of the angle’s orientation or relationship to other angles could have occurred (such as interchanging angles a and b). In such a case, the student might have mistakenly considered an angle opposite or another angle instead of the intended angle.

If there are no additional angles or mistakes mentioned, it seems like the initial answer of ( 123^\circ ) may actually be correct in the way angles ( b ) and the adjacent ( 57^\circ ) were visualized to produce a supplementary angle setup.

Please confirm the setup or provide more context if there’s any additional information that would lead to a different conclusion! @Antoine_Williams

[Antoine_Williams]

[StudyQbot]

To solve for ( x ) and ( y ) using the given angles (\angle 1), (\angle 2), and (\angle 3), we need to understand their relationships in the diagram.

Given:

• ( m\angle 1 = (114 - y)^\circ )
• ( m\angle 2 = 17^\circ )
• ( m\angle 3 = (x + 38)^\circ )

Based on the diagram, these angles could combine to form a straight line or another specific total, which is a crucial detail for setting up the correct equations.

Analyzing the Angle Relationships:

From the typical geometry perspective where angles form a straight line, the sum of angles along a line should be ( 180^\circ ).

Equation Setup:

• For a straight angle involving (\angle 1) and (\angle 2), it seems logical that:

  (114 - y) + 17 + (x + 38) = 180

  Which simplifies to:

  131 - y + x + 38 = 180
  x - y + 169 = 180
  x - y = 11

• To find individual measures where one of these parts does not depend geometrically on another, consider:
  [
  \begin{align*}
  x + 38 &= 90 & \quad \text{This commonly happens if angle 3 is perpendicular to another part of the line} \
  114 - y &= 90 & \quad \text{Angle 1 or another if perpendicular intersection} \
  \end{align*}
  ]

Select the Correct Option:

Analyzing for provided options with logical assumptions:

• Option A: ( 17 + x + 38 = 90 ) and ( 114 - y = 90 )

Keep in mind applying perpendicular setups to check these values against provided options. After assessment, as no specific perpendicular was listed for angles, utilizing straight line forms and potential perpendicular assumptions let us reach the selection.

Correct Choice: To ensure correctness based on analysis:

• Align correct option reads properly with logical deduction against available form: Option B or any result pre-established match to logical predict.

Hence, verify practical confirmation considering angles interactions within stated figure parameters to select the most suitable accordingly.

If you need further clarification, adjustments or breakdowns, please provide extra geometric relationships or constraints for re-evaluation. @Antoine_Williams

[Antoine_Williams]

[StudyQbot]

To find the correct selling price with a proper markup, we must first calculate the price using the given markup percentage and identify where the mistake might have occurred in the manager’s price.

Step-by-step Calculation:

1. Determine the Original Cost:

   • The item’s original cost is $16.

2. Calculate the Markup Amount:

   • The markup percentage is 25%.
   • To find the markup amount, multiply the original cost by the markup rate:
     \text{Markup Amount} = 0.25 \times 16 = 4

3. Calculate the Selling Price:

   • Add the markup amount to the original cost to find the selling price:
     \text{Selling Price} = 16 + 4 = 20

The correct selling price should be $20.

Manager’s Likely Error:

1. Misunderstanding the Markup Calculation:

   • The manager displayed a selling price of $4 instead of the correct $20. This must be a significant oversight.
   • A possible mistake could involve misinterpretation of adding the markup to the cost. They might have mistakenly subtracted the markup percentage of the cost rather than adding, which would not make practical sense.

2. Reversal or Typographical Error:

   • It is possible that this was a simple typographical or misplaced digit error.
   • The manager might have written $4 instead of $20 due to an incorrect placement of the digit, completely missing the base calculation.

The behavior indicates an oversight not intended, as no logical calculations align with $4 opposed the intended structure. This highlights importance of detailed checks and confirmations when assigning markup economics in product pricing.

Thus, the correct selling price should be $20 when accurately calculating and applying the 25% markup, avoiding computation mistakes. @Antoine_Williams

[Antoine_Williams]

[StudyQbot]

To find the percent markup, you need to determine the markup per shirt and then express that markup as a percentage of the original cost per shirt.

Step-by-step Calculation:

1. Determine the Original Cost Per Shirt:

   • The department store buys 400 shirts at a total cost of $7,200.
   \text{Cost per Shirt} = \frac{7200}{400} = 18

   So, each shirt costs $18 originally.

2. Determine the Selling Price Per Shirt:

   • Each shirt is sold for $20.

3. Calculate the Markup Per Shirt:

   • Subtract the original cost per shirt from the selling price:
   \text{Markup per Shirt} = 20 - 18 = 2

4. Calculate the Percent Markup:

   • The percent markup is calculated by dividing the markup per shirt by the original cost per shirt and then multiplying by 100 to convert to a percentage:
   \text{Percent Markup} = \left(\frac{2}{18}\right) \times 100
   • Calculate:
   \text{Percent Markup} = \left(\frac{2}{18}\right) \times 100 \approx 11.11
   • Rounded to the nearest whole number, the percent markup is 11%.

Therefore, the percent markup on each shirt is 11%, rounded to the nearest whole number. @Antoine_Williams