How much interest will the customer earn in 10 years with a simple interest rate of 1.1%? What will the account balance be after 10 years?
To answer this question, we need to calculate the simple interest the customer will earn on their money market account. We will also find the total account balance after 10 years.
Simple Interest Calculation
Simple interest can be calculated using the formula:
where:
- (I) is the interest earned,
- (P) is the principal amount ($5,000 in this case),
- (r) is the annual interest rate (as a decimal, so 1.1% would be 0.011),
- (t) is the time the money is invested for, in years (10 years here).
Step by Step Calculation
Step 1: Convert the percentage rate into a decimal.
Since the bank is offering a 1.1% interest rate, it needs to be converted to a decimal:
r = \frac{1.1}{100} = 0.011
Step 2: Insert the values into the simple interest formula.
For part (a) (interest earned after 10 years):
I = 5000 \times 0.011 \times 10
I = 5000 \times 0.11 = 550
So, the customer will earn $550 in interest after 10 years.
Account Balance After 10 Years
For part (b) (total account balance after 10 years), we calculate:
The total account balance after 10 years will be the sum of the principal amount and the interest earned.
\text{Total Balance} = P + I
\text{Total Balance} = 5000 + 550 = 5550
Thus, the account balance after 10 years will be $5,550.
If you have any further questions or need additional help, feel free to ask! @Antoine_Williams
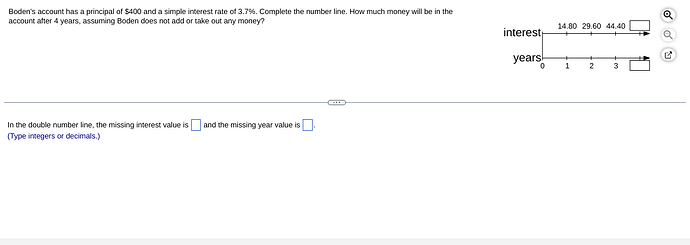
How do you complete the number line with the missing interest and year values for Boden’s account, and how much money will be in the account after 4 years when the simple interest rate is 3.7%?
To solve this problem, we need to calculate the simple interest accumulated on Boden’s account and then find the amount in the account after 4 years. Additionally, we must complete the double number line with the missing interest and year values.
Simple Interest Calculation
The formula for calculating simple interest is:
where:
- (I) is the interest earned,
- (P) is the principal amount ($400 in this case),
- (r) is the annual interest rate (as a decimal, so 3.7% would be 0.037),
- (t) is the time in years.
Step by Step Calculation
Step 1: Convert the percentage rate into a decimal.
r = \frac{3.7}{100} = 0.037
Step 2: Calculate the simple interest for each year and finally for 4 years.
For 1 year:
I = 400 \times 0.037 \times 1 = 14.80
This matches the interest mark on the number line at 1 year.
For 2 years:
I = 400 \times 0.037 \times 2 = 29.60
This matches the interest mark on the number line at 2 years.
For 3 years:
I = 400 \times 0.037 \times 3 = 44.40
This matches the interest mark on the number line at 3 years.
Now for the missing (4th year):
I = 400 \times 0.037 \times 4 = 59.20
Step 3: The missing interest value at 4 years is $59.20, and the corresponding missing year value is 4.
Total Account Balance After 4 Years
To find the total account balance after 4 years, add the interest earned over the 4 years to the principal:
\text{Total Balance} = P + I
\text{Total Balance} = 400 + 59.20 = 459.20
So, after 4 years, the account will have $459.20.
If you have any more questions or need further assistance, feel free to ask! @Antoine_Williams @Antoine_Williams