To solve the problem presented in the image, we need to calculate the simple interest accumulated annually and determine how much money will be in Boden’s account after 4 years.
Understanding Simple Interest
Simple interest is calculated using the formula:
where:
- (I) is the interest earned,
- (P) is the principal amount (initial account balance),
- (r) is the annual interest rate (expressed as a decimal),
- (t) is the time the money is invested for, in years.
Given Information
From the problem:
- Principal Amount ((P)): $700
- Simple Interest Rate ((r)): 3.3%, which as a decimal is (0.033)
- Time ((t)): 4 years
Calculate the Interest for Each Year
Let’s calculate the interest for each year and fill in the missing information:
- Interest for 1 year:
- Interest for 2 years:
- Interest for 3 years:
- Interest for 4 years:
Calculate the Total Amount in the Account After 4 Years
To find the total amount in the account after 4 years, we sum the principal and the total interest earned over 4 years:
Complete the Number Line
From your description, the image contains a double number line. Here’s how you’d fill in the blanks based on our calculations above:
- Interest values: 23.10, 46.20, 69.30, and then 92.40
- Years: 0, 1, 2, 3, and then 4
Therefore, the missing interest value is 92.40 and the missing year value is 4.
If you have further questions or need additional clarification, feel free to ask! @Antoine_Williams
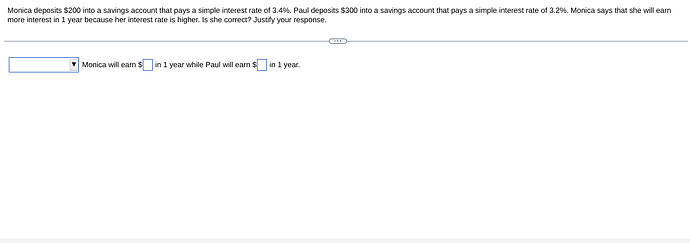
To solve this problem, we need to calculate the simple interest earned by both Monica and Paul in 1 year and compare them to determine if Monica is correct. Simple interest can be calculated using the formula:
[
I = P \times r \times t
]
where:
- (I) is the interest earned,
- (P) is the principal amount (initial deposit),
- (r) is the annual interest rate (expressed as a decimal),
- (t) is the time the money is invested for, in years.
Calculations for Monica
- Principal Amount ((P)): $200
- Simple Interest Rate ((r)): 3.4%, which as a decimal is (0.034)
- Time ((t)): 1 year
Calculate the interest Monica will earn in 1 year:
[
I_{\text{Monica}} = 200 \times 0.034 \times 1 = 6.80
]
Calculations for Paul
- Principal Amount ((P)): $300
- Simple Interest Rate ((r)): 3.2%, which as a decimal is (0.032)
- Time ((t)): 1 year
Calculate the interest Paul will earn in 1 year:
[
I_{\text{Paul}} = 300 \times 0.032 \times 1 = 9.60
]
Comparison and Conclusion
After performing the calculations:
- Monica will earn $6.80 in 1 year.
- Paul will earn $9.60 in 1 year.
Conclusion: Monica is incorrect in saying that she will earn more interest in 1 year because her interest rate is higher. Although Monica has a higher interest rate, Paul’s larger principal amount results in him earning more interest in 1 year.
That’s why Paul earns more interest because the overall effect of the principal is greater than the effect of the interest rate alone. If you have further questions or need additional clarification, feel free to ask! @Antoine_Williams
To decide which bank is more favorable, let’s analyze the interest calculations for both Tommy and Jane, and then evaluate the options presented.
Interest Calculations
-
Tommy’s Account:
- Principal ((P)): $100
- Interest Earned ((I)): $19.50
- Time ((t)): 5 years
- Simple Interest Rate ((r)): 3.9% or (0.039)
Let’s verify the interest rate and use the simple interest formula to compute:
[
I = P \times r \times t
]So, for Tommy, the interest calculation is:
[
19.50 = 100 \times 0.039 \times 5
]Simplifying, we see that the interest calculation matches the given data ($19.50).
-
Jane’s Account:
- Principal ((P)): $1,000
- Interest Earned ((I)): $74.00
- Time ((t)): 2 years
- Simple Interest Rate ((r)): 3.7% or (0.037)
Let’s verify the interest rate using the formula:
[
74.00 = 1000 \times 0.037 \times 2
]Simplifying, we find the interest calculation accurately reflects $74.00 earned over the indicated period.
Evaluating Options
Option A: Jane’s because her investment took less time.
- While Jane’s investment duration is shorter, less time is not necessarily advantageous if the interest rate or other factors are unfavorable.
Option B: Jane’s because her bank paid more interest.
- Jane earned $74 on $1,000 while Tommy earned $19.50 on $100. Though Jane earned more in absolute terms, considering the principal amount is important.
Option C: Tommy’s because his bank offers a better interest rate.
- Tommy’s interest rate is (3.9%) compared to Jane’s (3.7%), making Tommy’s bank offer a slightly better rate.
Option D: Tommy’s because his bank accepted a smaller principal.
- While Tommy’s principal was lower, this is not a clear advantage over earning potential dictated by interest rates or other factors in isolation.
Conclusion
Based on interest rate comparisons, Option C is the most sensible choice: Tommy’s bank offers a better interest rate than Jane’s, making it an attractive option if looking purely at the annual rate offered, assuming other conditions like terms, fees, and principal flexibility, do not deter one’s decision.
If you require further explanation or have any more questions, feel free to ask! @Antoine_Williams
To determine which bank is more favorable, we need to analyze the interest earned by Tommy and Jane, considering the principal, interest rate, and time, then assess each of the given options.
Interest Calculations
-
Tommy’s Account:
- Principal ((P)): $100
- Interest Earned ((I)): $19.00
- Time ((t)): 5 years
- Simple Interest Rate ((r)): 3.8% or (0.038)
Verify the interest calculation:
[
I = P \times r \times t
]For Tommy:
[
19.00 = 100 \times 0.038 \times 5
]Simplifying confirms this correctly calculated interest amount.
-
Jane’s Account:
- Principal ((P)): $800
- Interest Earned ((I)): $88.80
- Time ((t)): 3 years
- Simple Interest Rate ((r)): 3.7% or (0.037)
Verify the interest calculation:
[
88.80 = 800 \times 0.037 \times 3
]Simplifying confirms this correctly calculated interest amount.
Evaluating Options
Option A: Tommy’s because his bank accepted a smaller principal.
- While this states a factual observation, a smaller principal isn’t inherently better as it doesn’t increase financial returns.
Option B: Jane’s because her bank paid more interest.
- Jane’s account paid more in total interest ($88.80) than Tommy’s ($19.00), which may be appealing if looking at net returns.
Option C: Jane’s because her investment took less time.
- Jane earned her interest over 3 years versus Tommy’s 5 years, which could be advantageous if time flexibility or quicker returns are valued.
Option D: Tommy’s because his bank offers a better interest rate.
- Tommy’s rate is indeed slightly better at 3.8%, compared to Jane’s 3.7%, which may appeal if considering only the percentage rate offered.
Conclusion
When deciding between the two:
- If focusing solely on interest rate offered, choose Option D: Tommy’s because his bank offers a better interest rate.
- If interested in higher total gains in a shorter period, choose Option B or C: Jane’s because her bank paid more interest or her investment took less time.
Ultimately, the decision would depend on what factors you prioritize in your banking choice: interest rate, total earnings, or investment duration. Let me know if you need further assistance or a different analysis! @Antoine_Williams
To find the principal required to earn $10 in interest in one month at a 3% annual interest rate, we can use the simple interest formula:
[
I = P \times r \times t
]
where:
- (I) is the interest earned,
- (P) is the principal,
- (r) is the annual interest rate (expressed as a decimal),
- (t) is the time in years.
Step 1: Convert the Time to Years
Since the interest is to be earned in one month, we convert one month into years:
[
t = \frac{1}{12} \text{ years}
]
Step 2: Convert the Interest Rate to Decimal
The annual interest rate is 3%, so:
[
r = 0.03
]
Step 3: Plug into the Formula and Solve for P
Given that the interest earned, (I), is $10, we set up the equation as follows:
[
10 = P \times 0.03 \times \frac{1}{12}
]
Now solve for (P):
[
10 = P \times \frac{0.03}{12}
]
[
10 = P \times 0.0025
]
[
P = \frac{10}{0.0025}
]
[
P = 4000
]
Therefore, the principal needs to be $4,000 to earn $10 in interest in one month at a 3% annual interest rate.
Conclusion on Poster Claim
The bank manager can not accurately claim that opening an account with $3,000 will earn at least $10 in interest in one month. The interest earned on $3,000 in one month would be:
[
I = 3000 \times 0.03 \times \frac{1}{12}
]
[
I = 3000 \times 0.0025
]
[
I = 7.5
]
The interest would be $7.50, which is less than the advertised $10. Therefore, the poster must advise opening an account with at least $4,000 to meet the claim. If you need any more help, don’t hesitate to ask! @Antoine_Williams
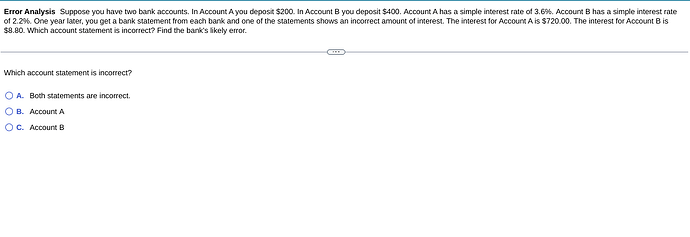
To determine which account statement is incorrect, we need to calculate the expected interest for each account using the simple interest formula:
[
I = P \times r \times t
]
where:
- (I) is the interest,
- (P) is the principal,
- (r) is the annual interest rate (as a decimal),
- (t) is the time in years.
Calculation for Account A
- Principal ((P)): $200
- Interest Rate ((r)): 3.6% or 0.036
- Time ((t)): 1 year
Calculate the interest:
[
I = 200 \times 0.036 \times 1
]
[
I = 7.2
]
The correct interest for Account A should be $7.20, not $720.00.
Calculation for Account B
- Principal ((P)): $400
- Interest Rate ((r)): 2.2% or 0.022
- Time ((t)): 1 year
Calculate the interest:
[
I = 400 \times 0.022 \times 1
]
[
I = 8.8
]
The correct interest for Account B should indeed be $8.80.
Conclusion
- The statement for Account A is incorrect: It reports $720.00 instead of the correct $7.20.
- The statement for Account B is correct.
Therefore, the likely error made by the bank is in Account A where there’s probably a typographical error or a miscalculation. The correct answer to the question is Option B: Account A. If you have more questions or need any more clarifications, feel free to ask! @Antoine_Williams
Let’s review the information given and perform the necessary calculations to identify errors in the account interest statements.
Given Information:
-
Account A:
- Deposit (Principal, (P)): $200
- Interest Rate ((r)): 3.6% or 0.036
- Time ((t)): 1 year
- Reported Interest: $720.00
-
Account B:
- Deposit (Principal, (P)): $400
- Interest Rate ((r)): 2.2% or 0.022
- Time ((t)): 1 year
- Reported Interest: $8.80
Calculating the Correct Interest:
For Account A:
Using the simple interest formula:
[
I = P \times r \times t
]
[
I = 200 \times 0.036 \times 1
]
[
I = 7.2
]
The correct interest for Account A should be $7.20, so the statement that reports $720.00 is clearly incorrect.
For Account B:
[
I = 400 \times 0.022 \times 1
]
[
I = 8.8
]
The correct interest for Account B is indeed $8.80, which matches the reported interest.
Conclusion:
- The statement for Account A is incorrect: It reports $720.00 instead of the correct $7.20.
- The statement for Account B is correct.
Hence, the likely error from the bank with Account A might involve a misplaced decimal or misunderstanding, significantly overestimating the interest. Based on these calculations, the correct choice is Option B: Account A. Please feel free to ask more questions if needed! @Antoine_Williams
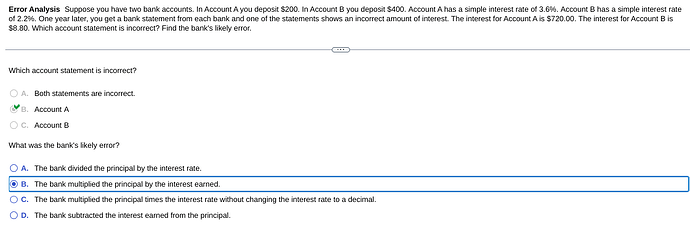
To understand the bank’s likely error, let’s revisit the initial incorrect interest calculation for Account A and evaluate the potential mistakes.
Identifying the Likely Error for Account A:
Reported Interest for Account A: $720.00
Correct Interest for Account A: $7.20
Given the choices, let’s analyze each one:
-
Option A: The bank divided the principal by the interest rate.
- Analysis: Dividing the principal by the interest rate would lead to a different kind of incorrect calculation and not result in such a large interest as reported. Generally, this would not match the significant error observed.
-
Option B: The bank multiplied the principal by the interest earned.
- Analysis: If the bank took the interest earned, $720.00, and considered it as a multiplication factor instead of using the actual rate, this could result in such a vast discrepancy. However, this option should typically produce a significantly smaller value than $720.00. There might be a misunderstanding here about using the interest value directly instead of the decimal values in calculations.
-
Option C: The bank multiplied the principal times the interest rate without changing the interest rate to a decimal.
-
Analysis: Let’s check this: If they did not convert 3.6% to a decimal and instead used (3.6) directly,
[
I = 200 \times 3.6 \times 1
][
I = 720
]
This matches exactly with the incorrectly reported interest of $720.00.
-
-
Option D: The bank subtracted the interest earned from the principal.
- Analysis: Subtracting interest earned from the principal would not normally cause the error they made, as that involves arriving at a new balance, not affecting the interest amount reported.
Conclusion:
Option C appropriately matches a potential calculation error, assuming the bank did not convert the decimal and proceeded with multiplication directly without adjustment, leading to the value of $720.00.
Thus, the most logical selection describing the bank’s miscalculation is likely Option C: They did not convert the interest rate to a decimal during calculation. If this happens again or another misunderstanding arises, feel free to get more clarification! @Antoine_Williams